We've been taught that greed is bad. If being greedy helped you solve a problem more quickly, would you consider that bad – or good?
To see how these concepts played out in our project for this client, please visit Increasing Customer Satisfaction by Improving Sales Order vs. Inventory Allocations.

Are there times when greedy is good? Well, greedy is certainly never good in the harmful Gordon Gecko "Greed is good!" sense. In some types of problem-solving, however, greedy can be very good, because it might be the only way to achieve a workable mathematical solution in a reasonable amount of time.
The problem underlying this month's case study appears simple on the surface – given a limited amount of inventory on hand and production jobs that will result in future inventory, determine how the inventory and jobs can be allocated to sales orders to satisfy the most customers.
What makes this problem difficult? One phrase – "to satisfy the most customers." You see, when you add words such as "most," "least," "maximize," or "minimize" to a problem, you transform it from a simple-to-solve allocation problem (allocate inventory to the sales orders, starting with the orders received earliest) to a hard-to-solve optimization problem.
Optimization problems fall into a category of computational problems called NP-complete. Mathematicians have proven that NP-complete problems are very hard to solve because solving such problems requires searching and evaluating every possible combination of inputs, and then selecting the best combination as the final result. Simply put, to optimally solve such problems, you use brute force to exhaustively search and evaluate all possibilities.
An easy-to-visualize example of an optimization problem is the knapsack problem. Imagine numerous items of varying sizes and weights – the goal is to pick the greatest number of items that both fit the knapsack, yet weigh no more than what a person could carry.
Consider the following illustration. For simplicity, let's assume all five items will fit in the knapsack – thus, our only constraint is that the weight of the items does not exceed 15 pounds.
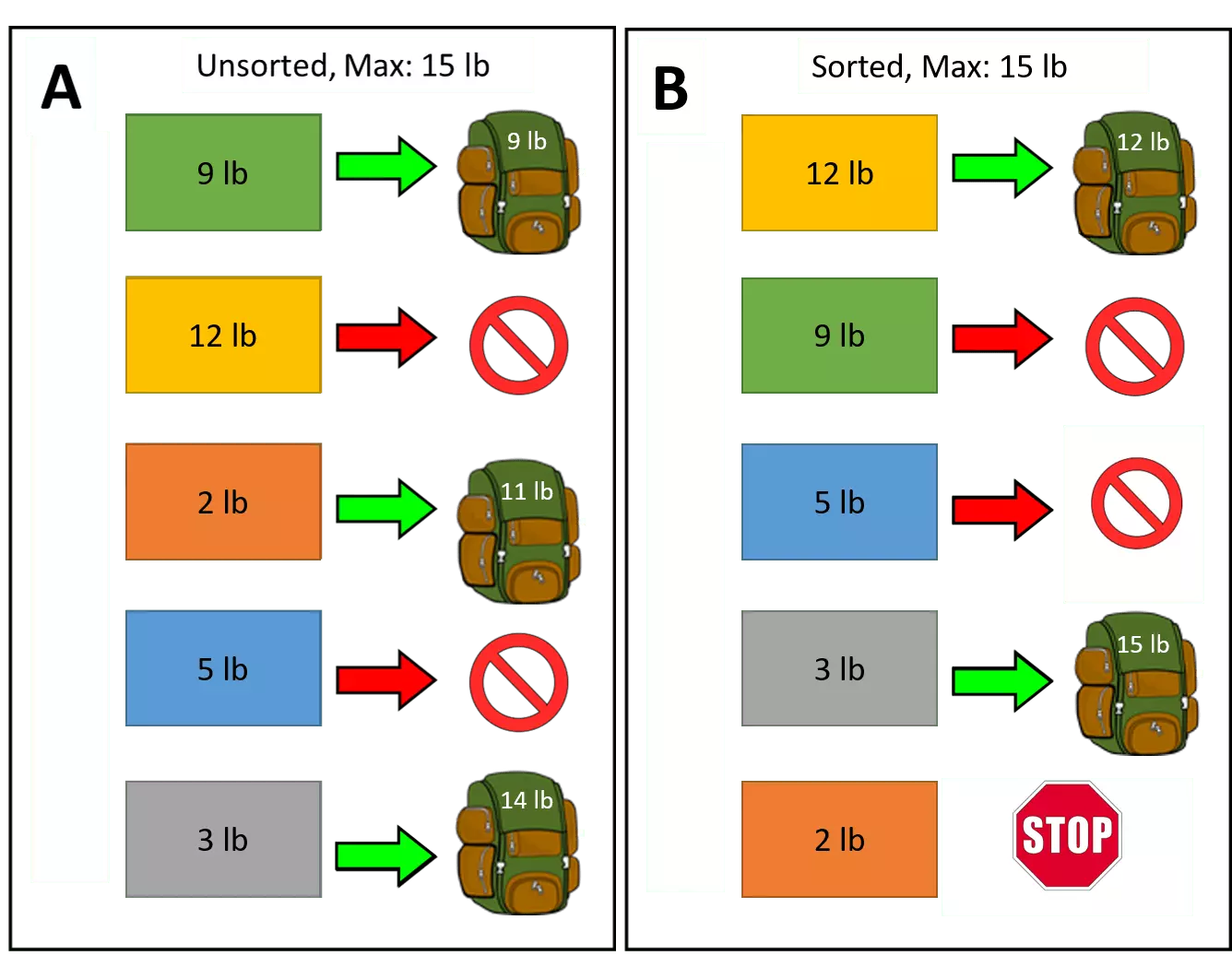
In Case A, the items are not sorted by weight, so the 9 pound item will be considered first. Its weight does not exceed 15 pounds, so we put it in the knapsack. At this point, we can put in items totaling no more than 6 pounds. The second item (12 pounds) exceeds 6 pounds – no need to consider it. The 2 pound item is next and it is less than 6 pounds, so we add it – our total is now 11 pounds, leaving 4 pounds to spare. The fourth item is 5 pounds, which would put us over the limit. The last item is 3 pounds, which can be put in the knapsack for a total of 14 pounds out of a 15 pound maximum.
In Case B, we have the same items, yet now they are sorted by descending weight. The first item is 12 pounds, so it goes in, leaving 3 pounds to spare. The second and third items are more than 3 pounds, so we ignore them. The fourth item is 3 pounds – we add it to the knapsack to achieve the 15 pound maximum. At this point, we are at the limit, so we can stop.
While these two cases were simple, they illustrate how sorting the data improves the search efficiency. In Case A, we had to make 5 decisions – "Yes" we can add this, or "No" we cannot – and evaluate ALL items. In Case B, we only had to make 4 decisions, and then we could stop after the fourth item – sorting by weight made the search 20% more efficient.
Perhaps counter intuitively, having constraints such as a maximum weight make brute force problems easier to solve. Why is this? Because once a particular combination of items exceeds the weight constraint, we can immediately stop looking for more combinations. Getting a "No" instead of a "Yes" to a constraint lets us prune all subsequent search branches from further consideration.
Solving knapsack-like problems – such as our inventory allocation problem – benefits from a greedy algorithm, where the data and decisions are structured in such a way to yield to a "Yes" or "No" decision as quickly as possible.
To solve our client's problem, we devised a search algorithm to creatively apply their three sales order constraints, and developed data structures for the inventory and jobs to satisfy ("Yes") or fail ("No") the constraints – quickly.
The result? Sales orders, inventory, and jobs for 225 stock items can now be evaluated, and a near-optimum solution can be found, in less than one minute. This routine runs on the client's main ERP (Enterprise Resource Planning) system and does not impact system performance, even during peak system usage.
If you have a business problem similar to this one and have been perplexed why no easy solution existed, just know such problems are inherently hard. Even so, very good – though not necessarily optimal – solutions can be devised. In fact, problems like these are right up our alley, so please contact me to discuss your needs.
Sincerely,
Todd L. Herman





